以前の続きです。
ドップラーセンサモジュールの動作確認ができたところで、つづいて電源制御回路の設計に入ります。

ブレッドボード上に、ドライブレコーダーの電源制御回路を組み上げたところです。

今回の心臓部となる、Microchip Technology Inc.の「PIC18F26K22」です。

もう一つ、秋月電子通商の、「3軸加速度センサモジュール KXR94-2050」(価格:850円)です。
DataSystemの「センサースイッチコントローラー」(SWC295Ⅱ)は、「ドップラーセンサ」(最大4つ接続可能)により、駐車中の人体の接近を検出し、ドライブレコーダーの電源を制御することができます。
しかし、「衝撃センサ」を搭載していないことから、残念ながら、他社のドライブレコーダーに具備されているような「当て逃げ」に対応することができません。
#もっとも、当てられる前からドップラーセンサが物体(被疑車両)の動きを検出し、ドライブレコーダーが動作しているのではないか、というハナシもありますが。
そこで、本回路では、卑劣な「当て逃げ」にも対応できるよう、「3軸加速度センサ」を用いて、車体に加えられた衝撃を検出できるようにしてみます。
秋月電子通商からは、複数の加速度センサが出ていますが、ほぼすべてのものが、+3.3V駆動のものとなっています。これは、低電圧駆動のマイコンとの接続を想定してのものと思われます。
PIC用に生成した+5Vから、+3.3Vに降圧してもよかったのですが、できるだけ基板上の部品点数を減らしたかったため、+5Vでも動作する、Kionix Inc.の「KXR94-2050」を選ぶことにしました。

開発環境です。
はじめに、「KXR94-2050」の動作を確認してみます。
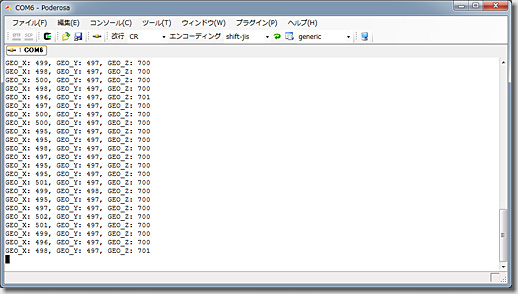
電源電圧は+4.997[V]で、X軸, Y軸, Z軸の出力電圧は、それぞれ、
+2.422[V], +2.413[V], +3.411[V]
で、各軸の出力電圧をA/D変換した値(GEO_X, GEO_Y, GEO_Z)は、それぞれ、
499, 497, 700
でした。
A/D変換は10bit精度(0~1,023)であることから、これらを電圧(0~+5V)に変換すると、
+2.437[V], +2.427[V], +3.418[V]
となり、かなりの精度でA/D変換されていることが分かります。
「KXR94-2050」のデータシートより、オフセット電圧(0G時の出力電圧)は2.500[V]、1Gあたりの出力振幅(感度)は1.000[V]であることから(いずれも電源電圧が+5.0V時)、X軸, Y軸, Z軸には、
-0.078, -0.088, 0.911
の加速度が掛かっていることが分かります。
なお、各軸とも、±0.020[V]の感度誤差、±0.075[V]のオフセット誤差(0G時の中心電圧)があります。(いずれも電源電圧が+5.0V時)
加速度センサモジュールは、デスク上に水平に置いてあることから、X軸とY軸は、ほぼ0G、Z軸は、ほぼ1Gとみることができます。
(この3次元ベクトルの大きさを計算したところ、ほぼ1となりました)
これらにより、駐車中に3軸の加速度を一定間隔で測定しておき、その3次元ベクトルの大きさが急激に変化した場合、車両に衝撃が加えられたものとみなし、ただちに前後のドライブレコーダーへの電源供給を開始するようにします。
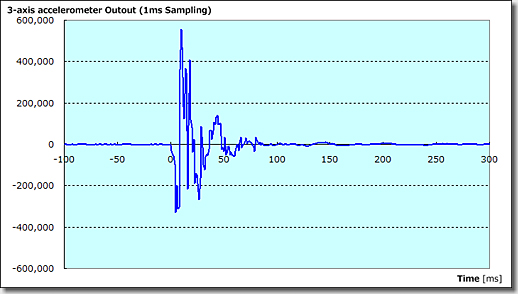
「3軸加速度センサからの出力波形」(サンプリング間隔:1ms)
車両に加えられた衝撃の、具体的な検出方法は、以下のとおりです。
車体に加えられた衝撃は、非常に短い時間で収束してしまうため、その昔、物理の時間に習った「力積」の考え方を導入することにします。
まず、3軸加速度センサからの出力を、単位時間(例えば1ms)毎にサンプリングし、逐次、リングバッファに格納していきます。
ここで、センサの各軸からの出力を、3次元ベクトルの大きさとして正規化しておくことにより、センサモジュールをどのような向きに設置したとしても、静止状態では「1G」となり、設置条件に関わらず、常に同じ結果を得ることができるようになります。
上記グラフは、センサモジュールをデスク上に設置し、衝撃を与えた際の、実際の出力波形を示したものです。(サンプリング間隔:1ms)
なお、3次元ベクトルを算出する際には、各軸からの出力を二乗し、加算し、平方根を取りたくなりますが、非力なPICに浮動小数点演算をさせるのは酷ですので(一定時間内に処理が終わらなくなる)、すべて整数演算の領域で処理を完了できるよう、プログラムを工夫しています。
また、計算量を軽減しつつ、計算中にオーバーフローを発生させないよう、有効ビット長を考慮し、short型(16bit)でもlong型(32bit)でもない、short long型(24bit)というデータ型を使っています。
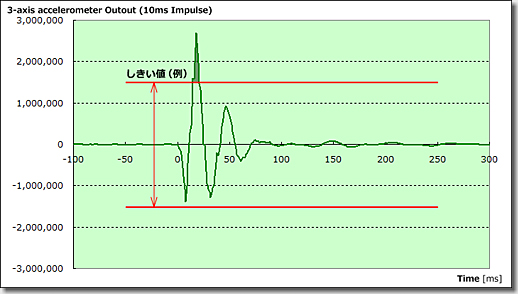
「3軸加速度センサからの出力の力積波形」(サンプリング間隔:1ms, 検出時間:10ms)
つぎに、リングバッファの値を、検出時間に対応する個数分(例えば10msとすれば、10個分)加算することにより、車両に与えられた衝撃の「力積」を算出することができます。
この「力積」(加えられたエネルギーの積分値)が、ある一定の「しきい値」を越えた場合、車体に衝撃が加えられたものと判定します。
上記グラフは、前述のグラフおいて、検出時間を10msとした際の、力積の算出結果を示したものです。(サンプリング間隔:1ms)
波形がかなりシンプルになり、衝撃を検出しやすいものとなっています。
(ここでも、オーバーフローを発生させないよう、有効ビット長に注意します)
本回路では、衝撃に対する感度を、ロータリースイッチにより、10段階(OFFと、0.1G刻みで+0.2Gから+1.0Gまで)に設定可能としています。

(Audi R8は、メーターパネル右端に、電圧計が付いています)
A/D変換を扱ったついでに、もう一つ工夫をしてみます。
駐車中にドライブレコーダーへの電源供給を開始する際、常時電源(BAT)の電圧を確認し、一定の電圧を下回っていた場合(+11.8V以下など)には、バッテリーが弱っているものとみなし、電源を供給しない(バッテリー上がりを防止する)ことにします。
#もっとも、Audi R8の場合は、V10という多気筒エンジンゆえ、そうとう大容量のバッテリーを積んでおり、ちょっとやそっとでは、バッテリーが上がらないのではないか、というハナシもありますが。
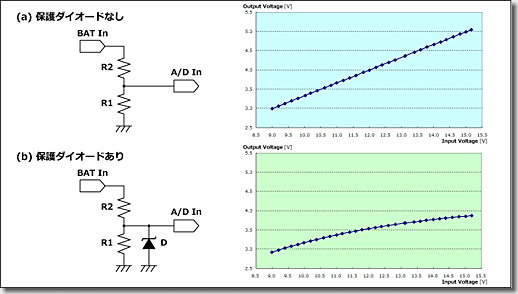
「保護ダイオードの有無による入力電圧の違い」
バッテリー電圧は、+14.0V前後(オルタネーター発電時)であることから、2つの抵抗で分圧し、PICに入力しています。
一般的には、回路(a)のような構成となりますが、本回路では、PICの入力に過大な電圧が掛かった際、入力を保護できるよう、回路(b)のように、ツェナーダイオードを並行に入れています。
回路(a)の場合は、入力と出力(バッテリー電圧とA/D変換入力電圧)との関係は、グラフ上段のように、リニア(線形)なものになりますが、回路(b)の場合は、ツェナーダイオードが入っていることにより、グラフ下段のように、ノンリニア(非線形)なものになります。
よって、A/D変換値(出力)からバッテリー電圧(入力)を推定するためには、入力を出力に変換する関数(y = f(x))を求め、さらに、その関数の逆関数(x = f-1(y))を求めることにより、出力から入力を推定することができるようになります。
ここでは、入力と出力との関係を実測し、Microsoft Excelを使って逆算数を求めることにします。
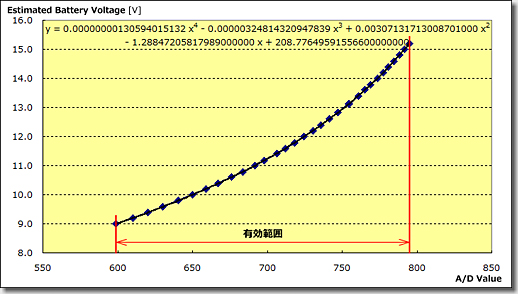
「逆関数によるA/D変換値からのバッテリー電圧の推定」(黒線が近似曲線)
まず、推定するバッテリー電圧の範囲を、+9.0V~+15.0Vとします。
#Audi R8の電圧計は、+8V~+16Vまで目盛りがありますが、そもそも放電停止電圧(+10.5V)を切ったら、セルモーターが回らないのではないか、というハナシもありますが。
安定化電源を使って、この電圧の範囲内で0.2Vピッチで電圧を発生させ、入力保護回路を通してPICに入力し、A/D変換した値を、実測していきます。
このA/D変換値とバッテリー電圧との関係を、Excelでグラフ化し、「近似曲線の追加」機能を使って、逆関数を求めます。
二次関数、三次関数と、項数を上げて試しましたが、四次関数で近似したところ、ほぼ誤差なく推定できることが分かりました。
この逆関数を得られれば、A/D変換値からバッテリー電圧を推定することができます。しかしながら、毎回、PICに四次関数の計算をさせるのは酷ですので、あらかじめA/D変換値に対応するバッテリー電圧を計算し、配列に格納しておき、A/D変換値から、その値に対応する配列の値を参照することにより、計算量を大幅に削減することができます。
具体的には、A/D変換は10bit精度であり、得られる値は0~1,023の範囲となることから、この値の範囲で逆関数を計算しておき、1,024個の値を、参照テーブル(short型)に格納しておくことにします。
ここで、逆関数の計算値を1,000倍しておけば、みなし固定小数点3桁となり、0.001V(1mv)の精度で推定することができます。
(とはいっても、理論上の精度は、約5mV(5V/1,024)であり、いたずらに倍率を上げても無意味ですので、計算中にオーバーフローを発生させないよう、有効ビット長を考慮し、倍率を決定します)
#いまからかれこれ四半世紀以上も前、アセンブラでPC-8801やPC-9801の3Dゲームを使るアルバイトをしていた頃、sin()やcos()などの計算を、浮動小数点を使わず、すべて整数(みなし固定小数点)でやっていた時に編み出したワザです。
(なにしろ、整数の乗算ですら遅かった時代、1フレーム(1/60s = 16.67ms)以内に、すべての処理を終えなければならなかったため、ありとあらゆる軽減ワザを考えました)
(ちなみに、当時の大卒の初任給よりはるかに稼いでいたため、大学院を修了し、いまの会社に入社後しばらくは、年間所得がだいぶ減りました)
(ここから、職人のクルマ道楽の日々が、始まることになります)
なお、言わずもがなですが、四次関数は、近似曲線に現れた以外の領域のどこかで、3回、折れ曲がっています。すなわち、近似に用いた領域以外のところでは、まったく無意味な値となってしまいます。
(実際、0近傍などの入力値の小さい領域、1,023近傍などの入力値の大きい領域では、とんでもない出力値となっています)
よって、有効範囲以外の値が入力された場合には、出力する値を補正する処理が必要となります。
今回の推定では、A/D変換値が600未満の場合には、強制的に9.0V、791以上の場合には、強制的に15.0Vとするようにしています。
(これにより、参照テーブルも、真面目に1,024個も用意する必要はなくなり、192個(600~791)で足りることから、データ量の軽減にも繋がる、という副次的なメリットも生まれます)
上記をインプリメントし、実際に動作させてみると、以下のような結果となりました。
| 印加電圧[V] | A/D入力[V] | A/D変換値 | 推定電圧[mV] |
| 9.00 | 2.925 | 600 | 9,018 |
| 10.00 | 3.169 | 649 | 9,977 |
| 11.00 | 3.369 | 691 | 10,986 |
| 12.00 | 3.530 | 723 | 11,939 |
| 13.00 | 3.665 | 750 | 12,936 |
| 14.00 | 3.766 | 772 | 13,928 |
| 15.00 | 3.854 | 791 | 14,955 |
| ※推定電圧は、逆関数の計算結果を1,000倍した値 | |||
A/D変換した電圧から、非常に精度高く、印加電圧を推定できていることが分かります。
本回路では、供給停止電圧を、DIPスイッチにより、2段階(10.8V, 11.8V)に設定可能としています。
また、衝撃を検出した際の電源供給時間を、DIPスイッチにより、4段階(30秒, 1分, 2分, 4分)に設定可能としています。
(電源供給中に新たな衝撃を検出した場合には、電源供給時間が延長されます)
ここまでの演算は、乗算・除算はほとんど使わず、多くを加算・減算で行い、一定時間(1ms間隔(1kHz)のタイマー割り込み)内に処理を完了できるよう、プログラムを工夫してあります。
(つづく)

 水冷PCのクーラント交換(EK Water Blocks)
水冷PCのクーラント交換(EK Water Blocks)



Post Comment