前回までの検証で、位相限定相関法により、2つの画像の上下方向（ティルト）と左右方向（パン）のズレを推定するとともに、風呂の中で思い付いた方法により、回転方向（ロール）のズレを推定し、補正してみました。
しかし、よくよく考えてみると（よくよく考えなくても）、画像Aと画像Bは、まったく同じ画像を合成していることが分かりました。
＃画像Bは、より実際の画像に近づいたように見えましたが、画像Aの左と右の画像をそれぞれ同じ角度だけ回転させ、位相限定相関法により合成しているため、2つの画像の間の回転方向のズレは補正されていません。
では、2つの画像があり、この2つの画像の間の回転方向のズレ（画像のロール角）を推定するには、どのようにすれば良いでしょうか。
すぐに思い付くのは、2つの画像を少しずつ回転させ、位相限定相関法により、2つの画像の間の相関係数が最も高くなる角度を拾う方法があります。
しかし、この方法では、分解能を1°とすると、180回も計算しなければならず、とても実時間には間に合いません。仮に二分法が上手くいくとしても、9回も計算しなければなりません。
なにか上手い方法がないかと探していたところ、「対数極座標変換」（Log-Polar Transform）という方法があることが分かりました。
これは、霊長類の視覚の「中心視」をモデル化したものです。（なぜに「中心視」なのかは、後ほど）
対数極座標変換は、以下のような式で表されます。
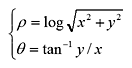
変換後の画像は、変換前の画像のどの画素に対応するかを計算することから、上記の式を逆変換すると、以下のようになります。
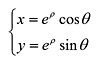
さっそく、評価用の画像を対数極座標変換してみます。
原画像（512×512）。
変換後の画像。
縦方向にグニャ～っとなっていますが、原画像がなんとなく推測できそうなところと、まったく推測できないところがあります。
プログラム（一部）です。（LogPolarImage.cpp）
（変換後の画素から変換前の画素の参照には、バイリニア補間を使っています。画素の参照は、ポインタを使って微妙に高速化しています）
すこし脱線しますが、なぜにこの対数極座標変換が、「霊長類の中心視をモデル化したもの」なのか、つぎの画像をご覧ください。
左側の画像を、いったん対数極座標変換し、さらに逆変換したものが、右側の画像になります。
中心付近の情報は、逆変換後も保存されていますが、外周にいくに従って、次第に情報が失われていくのが分かります。
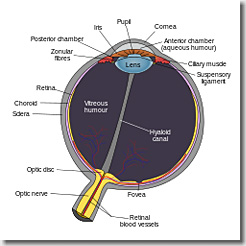
（画像は、Wikipediaから拝借）
なんとなく、眼底に映った写像のようにも見えます。
人間は、外界を見る時に、全体を見ているようで、実は全体を見ていなくて、「視線の先のものはしっかり見ているけれども、周りのものはぼんやりと見ている」という特性がありますが、これがうまく表されています。
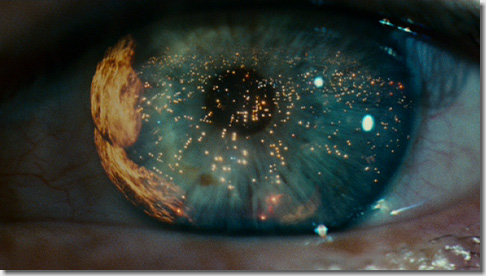
（画像は、映画「Blade Runner」から拝借）
目に映るすべてのものを見ていると、脳が情報を処理しきれなくなってしまうため、必要とするところ以外の部分は、ある程度情報を捨てているのかも知れません。
そう考えると、数式に含まれた意味が“イメージ”できて、面白いですね。0xF9C6
さて、話を本論に戻します。
以下、画像のロール角を変えた時の変化が分かりやすいよう、原画像と変換後の画像を並べてみます。
（対数極座標変換後の画像は、右に90°回転させてあります）
初期状態（角度0°）。
45°回転。
90°回転。
違いが分かりましたでしょうか。
実座標における「回転方向の動き」は、対数極座標における「横方向の動き」（時計回りに90°回転させてあるので、実際には縦方向の動き）に変わっています。
ここが重要です。0xF9C5
〔関連情報〕
・【OpenCV】位相限定相関法による画像マッチング(3)
・【OpenCV】位相限定相関法による画像マッチング(2)
・【OpenCV】位相限定相関法による画像マッチング(1)
・【OpenCV】ステレオカメラからの画像入力(1)
・【OpenCV】位相画像の生成
・【OpenCV】広角レンズの歪み補正
| 14 Related Entries | |
 Previous 【OpenCV】位相限定相関法による画像マッチング(3) | Next   【OpenCV】回転不変位相限定相関法による画像マッチング(1) |
SOARISTO at 21:31:24
|
Comment(0)
|
Trackback(0)Link URL: https://www.soaristo.org/blog/archives/2015/02/150221.php
Post Comment