前回の続きです。OpenCVの関数を使って、位相画像を生成してみます。
画像をfとすると、fの離散フーリエ変換（Discrete Fourier Transform）は、以下の式で表されます。
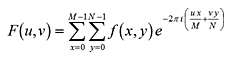
得られた空間周波数スペクトル（複素平面）を、その振幅の絶対値で除することにより正規化します。
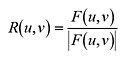
この複素平面を逆離散フーリエ変換することにより、位相画像rを得ます。
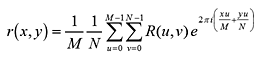
複素平面における正規化により、振幅信号（情報）が1になり、位相信号（情報）が残ることになります。
さっそく検証してみます。
まずは評価用の画像。
＃画像処理の世界では最も有名(?)な女性、Lenaさんです。0xF9CB
空間周波数スペクトルの画像。
（ハン窓を掛けてから離散フーリエ変換（cvDFT()）し、四象限を入れ替え（cvShiftDFT()）てあります）
処理後の画像。
（複素平面を振幅で正規化し、逆フーリエ変換しています）
振幅（濃淡）情報が失われ、位相の変化（輪郭）が強調された画像になっています。
この「輪郭の強調」（エッジの抽出）が、この後の処理で重要になります。
ということで、久しぶりにプログラムをゴリゴリ書いてみました。（PhaseImage.cpp）
（たいした長さではありませんが）
特段、難しいことはしていません。コメントを読めば、ご理解いただけると思います。
OpenCVは、配列操作のための関数が揃っているので、かなり楽チンです。
実画像で試してみます。
原画像。
位相画像。
原画像。
位相画像。
〔関連情報〕
・【OpenCV】広角レンズの歪み補正
| 14 Related Entries | |
 Previous 【OpenCV】広角レンズの歪み補正 | Next   【OpenCV】ステレオカメラからの画像入力(1) |
Posted by 
SOARISTO at 21:32:32
|
Comment(0)
|
Trackback(0)
Link URL: https://www.soaristo.org/blog/archives/2015/02/150211.php
SOARISTO at 21:32:32
|
Comment(0)
|
Trackback(0)Link URL: https://www.soaristo.org/blog/archives/2015/02/150211.php
Post Comment