さて、前回までで、「回転不変位相限定相関法」（RIPOC; Rotation Invariant Phase Only Correlation Method）の実装と検証を行ってきました。

　検証に用いた2つの画像は、同一の画像から切り出したものであり、外部からの撹乱などの影響のない、いわば“きれいな”画像でした。精度よくシフト量とロール角が推定できるのは、ある意味当たり前といえば当たり前でした。

　そこで、いよいよ、実際の画像に適用し、効果を検証してみます。

　評価用に用いるのは、いつもの2つの左右画像。（1920×1080）

　これを、端から1/4ずつ切り出し、照合します。（480×1080）

　OpenCVでは、画像（配列）に対して着目領域（ROI; Region Of Interest）を設定できるため、取り扱いが非常に簡単です。

　前回までの検証により、

1. 画像をフーリエ変換し、振幅で正規化した後、逆フーリエ変換すると、位相情報を表す画像（位相画像）を得ることができる。
2. 2つの画像の位相情報の畳み込み（合成積）を取り、振幅で正規化した後、逆フーリエ変換すると、2つの画像の間のシフト量（X方向, Y方向）を得ることができる。
   （これを、「位相限定相関法」という）
3. 実座標を対数極座標に変換すると、実座標における回転方向の動きを、対数極座標における縦方向の動きとして表すことができる。

ということが分かりました。

　これらを組み合わせて、2つの画像の間の回転方向のズレ（画像のロール角）を推定してみることにします。

　「回転不変位相限定相関法」（RIPOC; Rotation Invariant Phase Only Correlation Method）です。

　回転不変位相限定相関法の処理手順は、以下のようになります。

　まずは、原画像（1920×1080）から、評価用の画像を作ります。

　青枠のところを切り出し、画像Aとします。さらに、X方向に29.5, Y方向に14.5シフトし、反時計回りに19.0°回転させて赤枠のところで切り出し、画像Bとします。

　2つの画像の間のシフト量およびロール角は、リサイズ後の画素に換算すると、

　　　X: 19.796[pixel]

　　　Y: 9.730[pixel]

　　　θ: 19.0[degree]

となります。

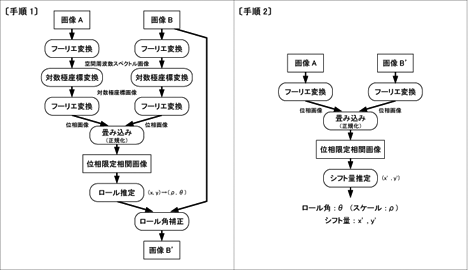
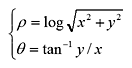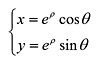　前回までの検証で、位相限定相関法により、2つの画像の上下方向（ティルト）と左右方向（パン）のズレを推定するとともに、風呂の中で思い付いた方法により、回転方向（ロール）のズレを推定し、補正してみました。

　しかし、よくよく考えてみると（よくよく考えなくても）、画像Aと画像Bは、まったく同じ画像を合成していることが分かりました。

＃画像Bは、より実際の画像に近づいたように見えましたが、画像Aの左と右の画像をそれぞれ同じ角度だけ回転させ、位相限定相関法により合成しているため、2つの画像の間の回転方向のズレは補正されていません。

　では、2つの画像があり、この2つの画像の間の回転方向のズレ（画像のロール角）を推定するには、どのようにすれば良いでしょうか。

　すぐに思い付くのは、2つの画像を少しずつ回転させ、位相限定相関法により、2つの画像の間の相関係数が最も高くなる角度を拾う方法があります。

　しかし、この方法では、分解能を1°とすると、180回も計算しなければならず、とても実時間には間に合いません。仮に二分法が上手くいくとしても、9回も計算しなければなりません。

　なにか上手い方法がないかと探していたところ、「対数極座標変換」（Log-Polar Transform）という方法があることが分かりました。

　これは、霊長類の視覚の「中心視」をモデル化したものです。（なぜに「中心視」なのかは、後ほど）

　対数極座標変換は、以下のような式で表されます。

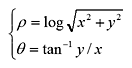
　変換後の画像は、変換前の画像のどの画素に対応するかを計算することから、上記の式を逆変換すると、以下のようになります。

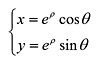
　さっそく、評価用の画像を対数極座標変換してみます。

　原画像（512×512）。

　変換後の画像。

　縦方向にグニャ～っとなっていますが、原画像がなんとなく推測できそうなところと、まったく推測できないところがあります。

　前回までの検証で、位相限定相関法により、2つの画像の上下（ティルト）と左右（パン）のズレを補正できることが分かりました。

　前回の結果です。

　左右2つの画像のシフト量は、

　　　X: -192.355[pixel]

　　　Y: 46.7339[pixel]

でした。

　カメラ（αNEX-5R）を三脚の雲台に固定し、そのまま左右にパンしたはずなのですが、なぜこれだけ上下にズレてしまったのか、このズレを補正するにはどうすれば良いか、さまざまに考えを巡らせていたところ、風呂に浸かっている時に、ハタと気づきました。0xF9A0

　この上下のズレは、「カメラのロール（左右の回転）によるものではないか」と。

　カメラを雲台に載せて左右にパンしたので、「ロールによるズレはないはずだ」というのは、単なる思い込みでした。

　思い起こせば、確かに、雲台に水準器は付いていましたが、公道のド真ん中で、歩行者信号が青の時に、横断歩道の上から急いで撮ったので、水準器を合わせているヒマはありませんでした。

　ゆえに、水平が出ていないまま（カメラがロールしたまま）左右にパンしたため、上記のような上下のズレが生じてしまったようです。

　さて、この上下のズレを生じさせたカメラのロール角ですが、どのようにすれば求められるでしょうか。

　原画像の大きさは1920×1080で、上下のズレは、上記のとおり、Y方向に46.7339[pixel]なので、回転軸を画像の中心（960, 540）とすると、ロール角は、

　　　tan^-1(46.7339/960) = 2.787°

と求められます。

　試しに、左右それぞれの画像を2.787°回転させ、改めて位相限定相関法によりシフト量を推定し、2つの画像を合成すると、以下のようになります。

（クリックで拡大）

　これまで、位相画像の生成や、位相限定相関法（POC; Phase Only Correlation Method）の実装などを、シコシコとやってきた訳ですが・・・。

　なんとっ！　OpenCVの関数として、位相限定相関法が提供されていることが分かりました。

＃もっと早く気づけば良かった。0xF9D3
　（まぁ、原理が分かっただけでも良しとしましょう）

　位相限定相関法の関数（phaseCorrelate()）を含むソースファイルは、以下のフォルダに格納されています。

　　　\opencv-2.4.10\sources\modules\imgproc\src\phasecorr.cpp

　関数phaseCorrelate()自体の解説は、こちら。

　　　・Motion Analysis and Object Tracking — OpenCV documentation

　評価用の画像の原画像（1920×1080）です。

　前回同様、青枠から赤枠へのシフト量を推定します。

　プログラムです。（PhaseOnlyCorrelation.cpp）

　関数phaseCorrelate()は、2つのグレースケール画像と、窓関数の配列を与えると、X方向およびY方向の「シフト量」と、5×5のマトリクスの重心における「ピーク値」を返します。
（ピーク値はオプション）

　窓関数は、サンプルに準じて、ハニング窓（hanning window）を使っています。